Classification 文章筆記整理 - ft. Decision Tree, Random Forest, SVM
1102 機器學習
這篇文章是學習時整理的一些筆記,讓自己複習時方便,文章內容為上課之內容及閱讀清單之整理
監督式學習最常處理的兩個問題:分類、迴歸
當預測的數值為連續的我們稱為迴歸,若是離散的,我們稱為分類
簡單來說,
迴歸就是找一條線,而該線盡可能的通過所有的資料點
分類就是把資料分到指定的幾個分類中
本篇主要是在講迴歸,若要看分類的在另外一則文章喔!
linear 文章筆記整理分類問題
- 判斷資料是否屬於某一個類別
- 可分為二元分類(binary)或多元分類(multi-class)
- 屬於監督式學習的一種
Logistic regression 雖然有迴歸的名稱,但實際上是一個二元分類(Binary classification)演算法
接下來介紹幾個不同的分類模型~
常見的演算法有決策樹、邏輯迴歸、SVM、樸素貝斯葉
Decision Tree 決策樹
決策樹就像一棵樹一樣,而每個節點都代表一個特徵,依據特徵一步一步的分類
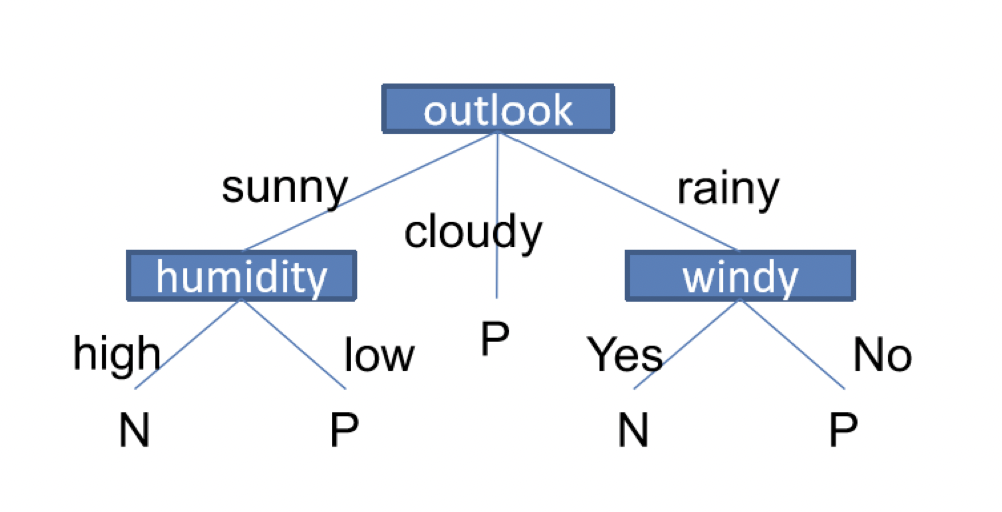
決策樹會依據訓練資料產生一棵樹,決策樹演算法可以使用不同方法來評估分枝的亂度,如information gain, gain ratio, gini index,依據訓練資料來找出最適合的規則。
決策樹如何生成的?
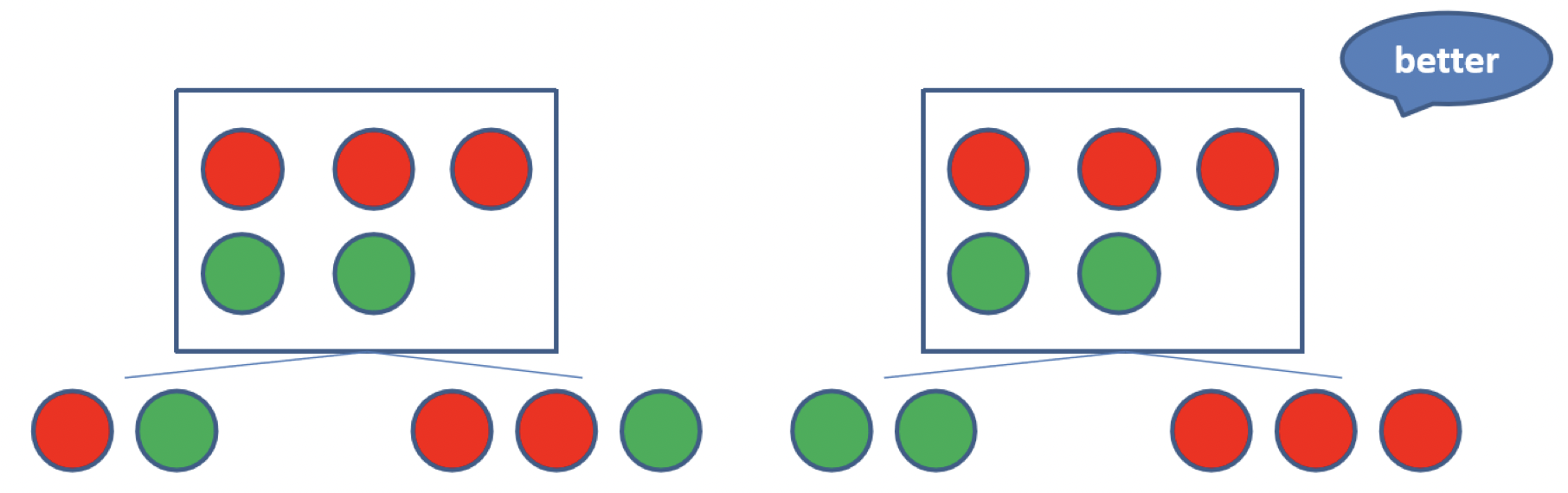
決策樹是以貪婪演算法來決定每一層要用哪一個特徵分類,最好的情況是使用某一個特徵後,所有的資料都可以很精準的被分類,如下圖所示:(使用右邊的特徵分類會更好)
貪婪演算法是一種在每一步選擇中都採取在當前狀態下最好或最佳(即最有利)的選擇,從而希望導致結果是最好或最佳的演算法 - wiki
- Tree is constructed in a top-down recursive divide-and-conquer manner
- attributes are categorical(if an attribute is a continuous number, it needs to be discretized in advance)
Divide-and-Conquer分治算法,先將原問題分解成「「問題相同但規模小」的子問題,再反覆重複這個過程直到問題規模小到可以求解為止
- At start, all the training examples are at the root
- Examples are partitioned recursively based on selected attributes
- Test attributes are selected on the basis of a heuristic or statistical measure (eg. information gain): maximizing an information gain measure)
favoring the partitioning which makes the majority of examples belong to a single class
Conditions for stopping partitioning:
- all samples for a given node belong to the same class
- There are no remaining attributes for further partitioning - majority voting is employed for classifying the leaf
- There are no samples left
決策樹建構議題
- 分裂的準則 Split criterion (goodness function)
- used to select the attribures to be split at a tree node during the tree generation phase
- different algorithms may use different goodness functions:
- information gain used in ID3/C4.5
- Gini index used in CART
- 分枝的方案 Branch scheme
- determining the tree branch to which a sample belongs
- binary or k-ary splitting
- 何時停止分枝
- impurity measure
- 訂定標籤的規則
- a node is labeled as the class to which most samples at the node belongs
決策樹亂度評估準則
我們需要訂定一個指標、標準來評估決策樹的每個節點,常用的指標有:
- Information gain 資訊獲利
- Gain ratio 吉尼獲利
- Gini index 吉尼係數 (Gini impurity 吉尼不純度)
以上的指標都是在衡量一個序列中的亂度,數值越高代表越混亂
我們的目標是找出一個規則,透過從訓練資料中找出規則讓每一個決策都可以使訊息增益最大化
How to use a Tree?
- Directly
- test the attributes value of unknown sample against the tree
- a path is traced from root to a leaf which holds the label
- Indirectly
- decision tree is converted to classification rules
- one rules is created for each path from the root to a leaf
- IF-THEN is easier for humans to understand
評估分割資訊量
常見的評估資訊分割量方法有兩種:
- Information gain
- Gini impurity
Information gain主要的算法是在計算「熵」(entropy),因此決策樹分割後後的資訊量要越小越好
而Gini的數值越大代表序列越混亂,值介在0~1之間,其中0代表資料被完美分類
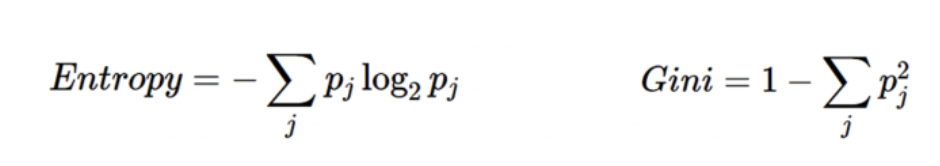
Information gain 資訊獲利
「熵」(entropy)計算是information gain的一種方式,在了解information gain之前先介紹一下entropy的計算
有關熵的詳細介紹前往這則文章
下圖中p代表是的機率、q代表否的機率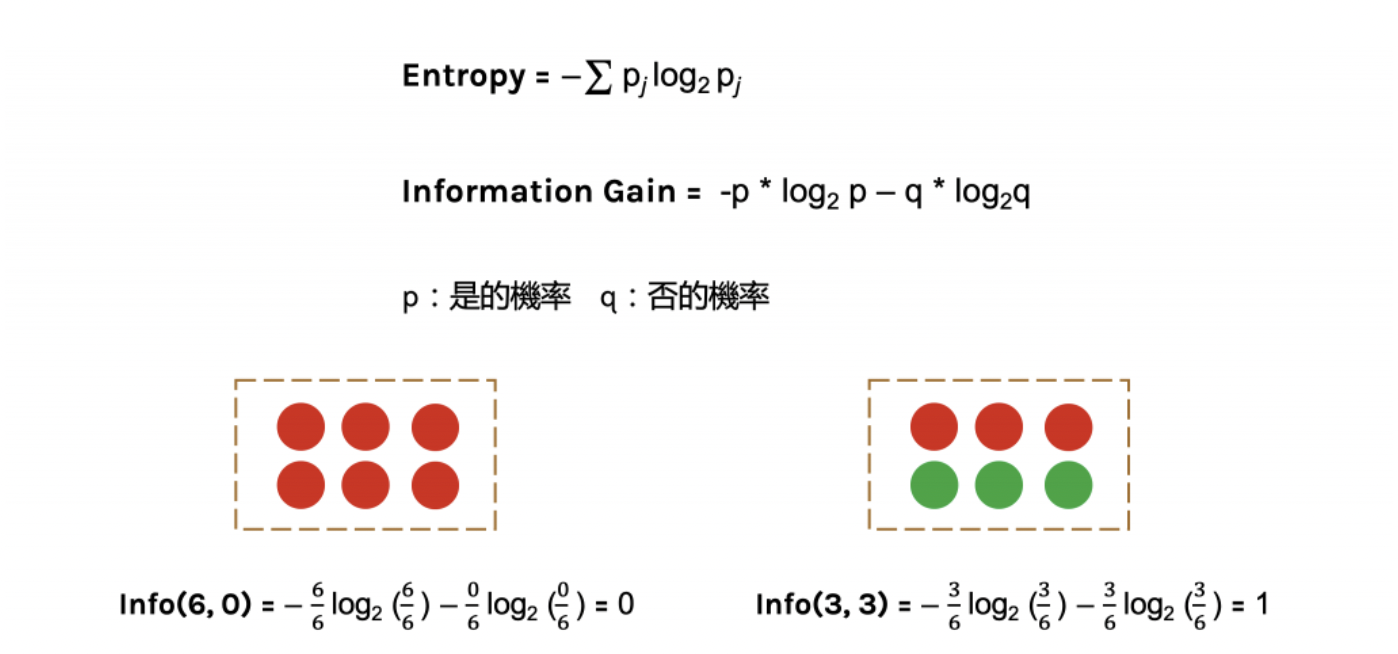
當資料被分類一致的時候entropy為0,當資料各為一半的時後為1
再舉一個例子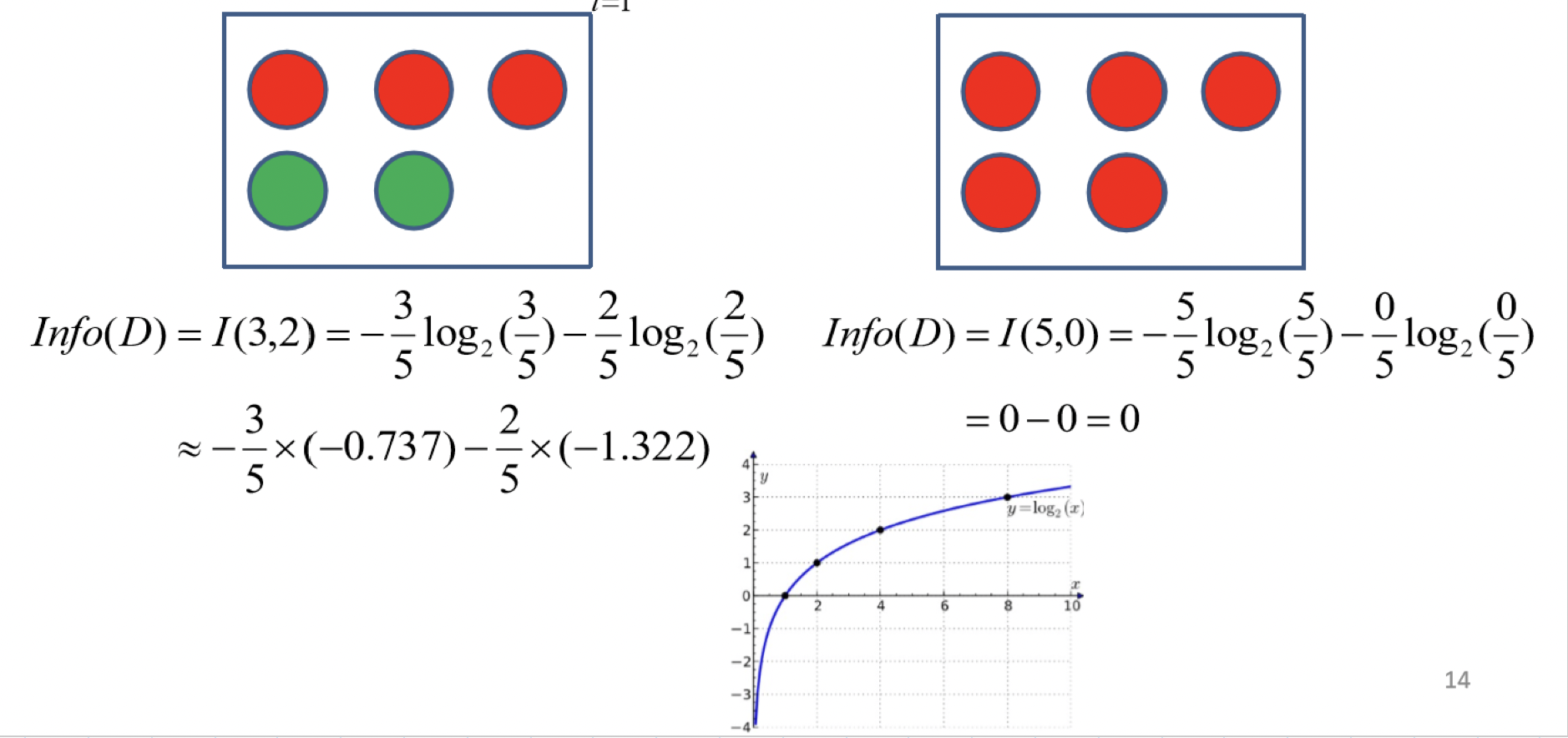
則information gain 就可以這樣得來囉~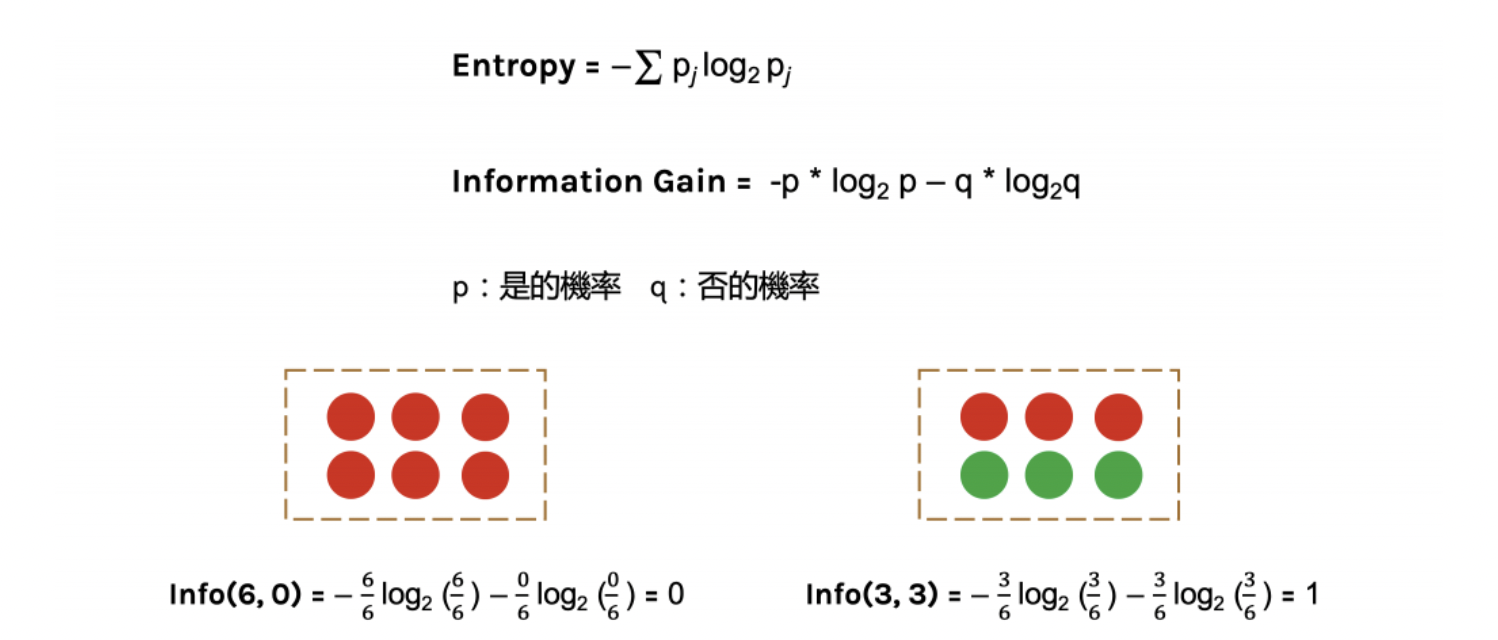
Gini impurity 不純度
不純度是另外一種衡量資訊亂度的方式,他的數值越大代表資料越混亂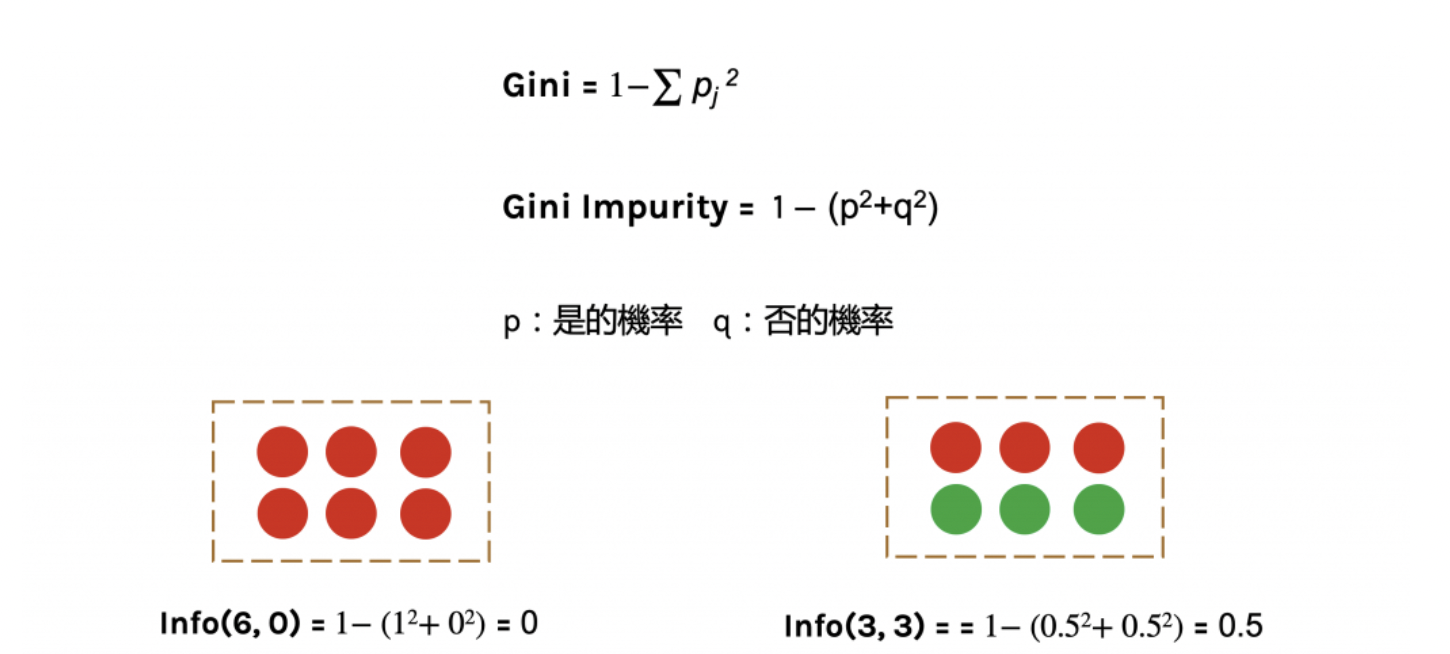
Ramdom Forest 隨機森林
隨機森林的基本原理是結合多個CART決策樹,並加入隨機分配的訓練資料,結合多個「弱學習」來建構一個「強學習器」的概念,這種方法又稱為Ensemble Method
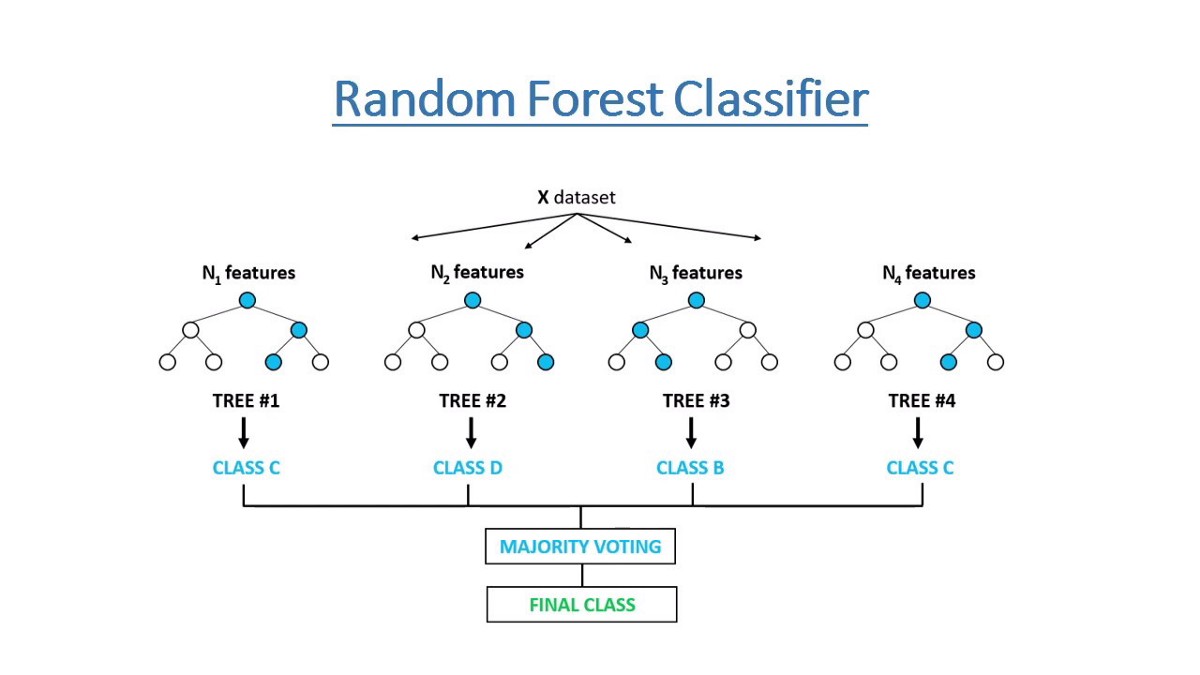
- each classifier in the ensemble is a decision tree classifier and is generated using a random selection of attributes at each node to determine the split
- during classification, each tree votes and the most popular class is returned
樹的產生
不過若是我們想要產生多個不同的CART樹,我們就要產生不同的數據集,產生數據集的做法有兩種:
- Bagging(Boostrap Aggregation)
- Boosting
Bagging(Boostrap Aggregation)
此種作法是從原有的數據集內重新取樣產生新的數據集,且取的過程是「均勻且可重複取樣的」
這種做法會從原有的數據集內產生新的k個數據集,再訓練出k個分類器(CART樹),每次取出的數據都會放回原數據集,因此彼此之間可能會有資料重複,不過每個樹還是會有不同的樣本,因此每棵樹還是不同的,最後每個樹的權重統一由投票方式決定(Majority vote)
Boosting
和Bagging方式類似,不過更強調「對錯誤的部分加強學習」,將舊分類器錯誤資料的權重提高,加重對錯誤資料的訓練,訓練出新的分類器,這樣新的分類器就會學習到錯誤資料的特性。
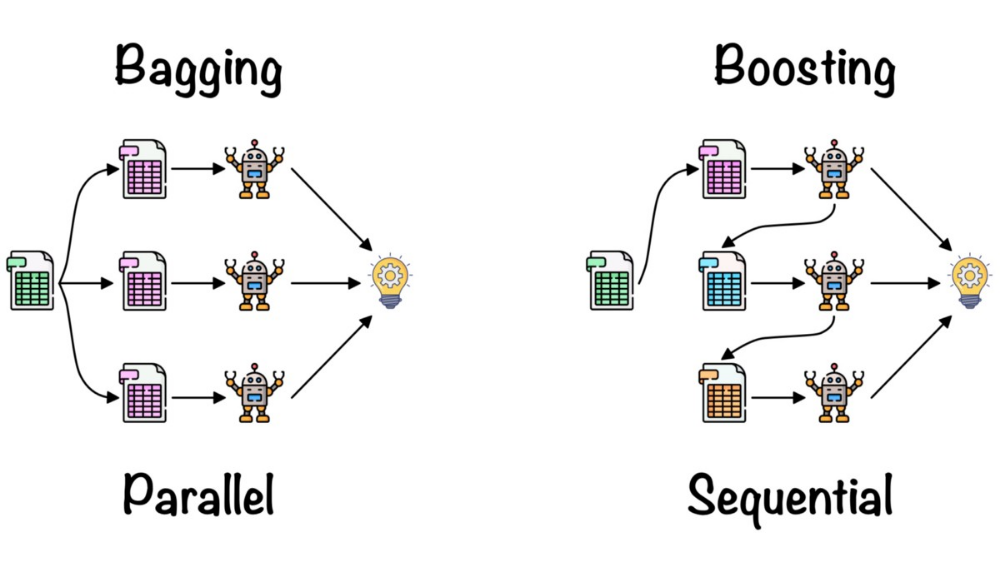
(boosting會將上一個產生的樹分類錯的資料加入訓練)
森林的產生
故綜合上述所說的,產生隨機森林的步驟就是:(以bagging說明)
- 從原數據集中取出n筆數據產生一個新的數據集,取完後放回
- 用先前產生的新數據集訓練一個決策樹,對每個節點選取特徵後分割該節點
- 重複k次步驟1、2會得到k個決策樹
- 綜合所有決策樹以多數決的方式決定最後分類
Support Vector Machine 支援向量機
下圖每條線都可以將資料點分類,不過哪一條更好呢?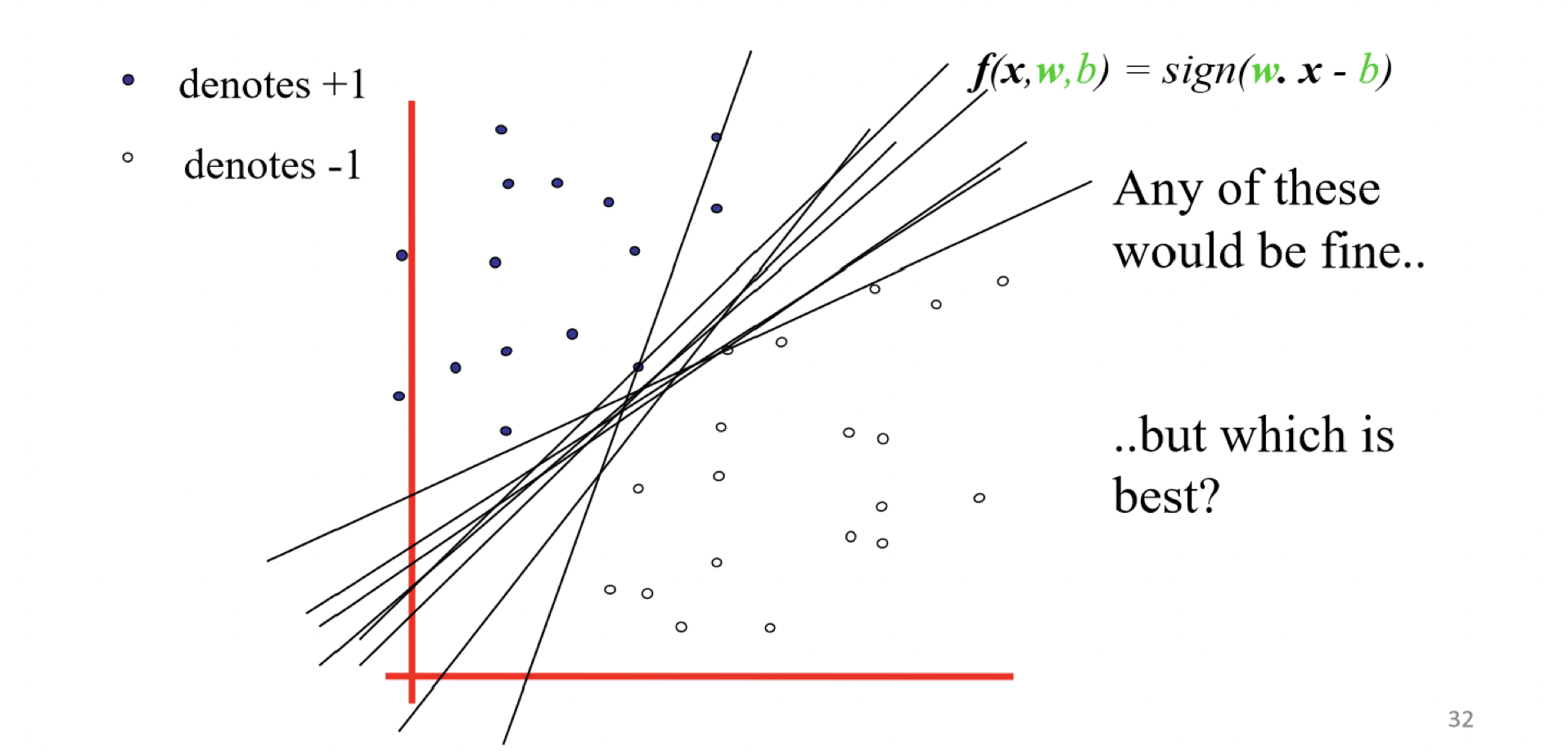
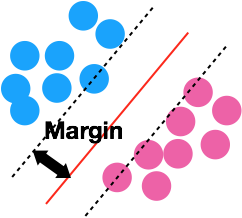
那SVM是怎麼得到那條很好的線呢?以直線來說,首先紅色的線會創造兩條黑色平行於紅色線的虛線,並讓黑線平移碰到最近的一個點,紅線到黑線的距離稱為Margin,而SVM就是透過去找Margin最大的那個紅線,來找最好的線reference
定義線性分類器的margin,在沒有碰到資料點內增加寬度,目標是最大化這個寬度(Linear SVM)
而碰到margin的點即為support vector(支援向量)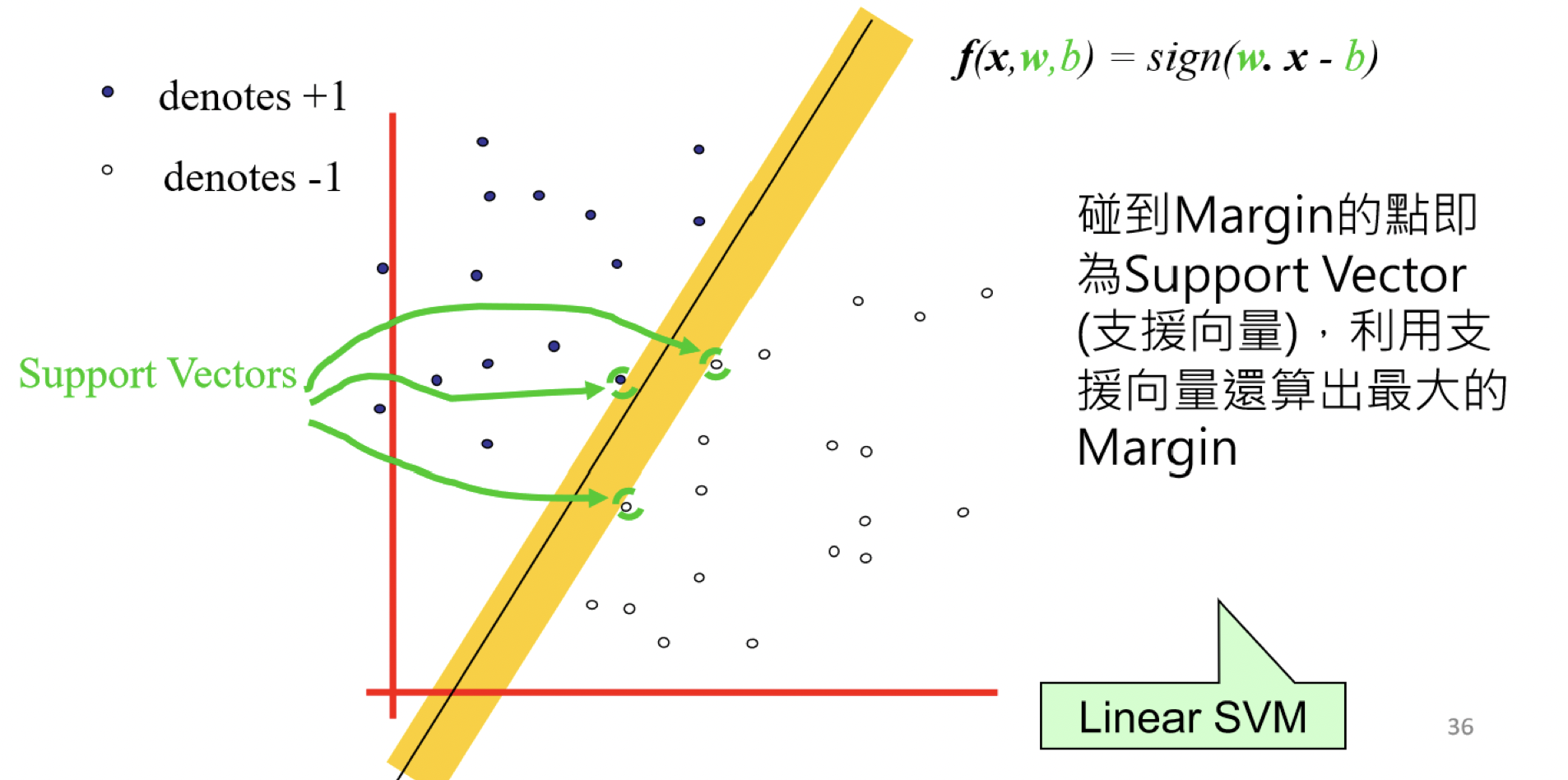
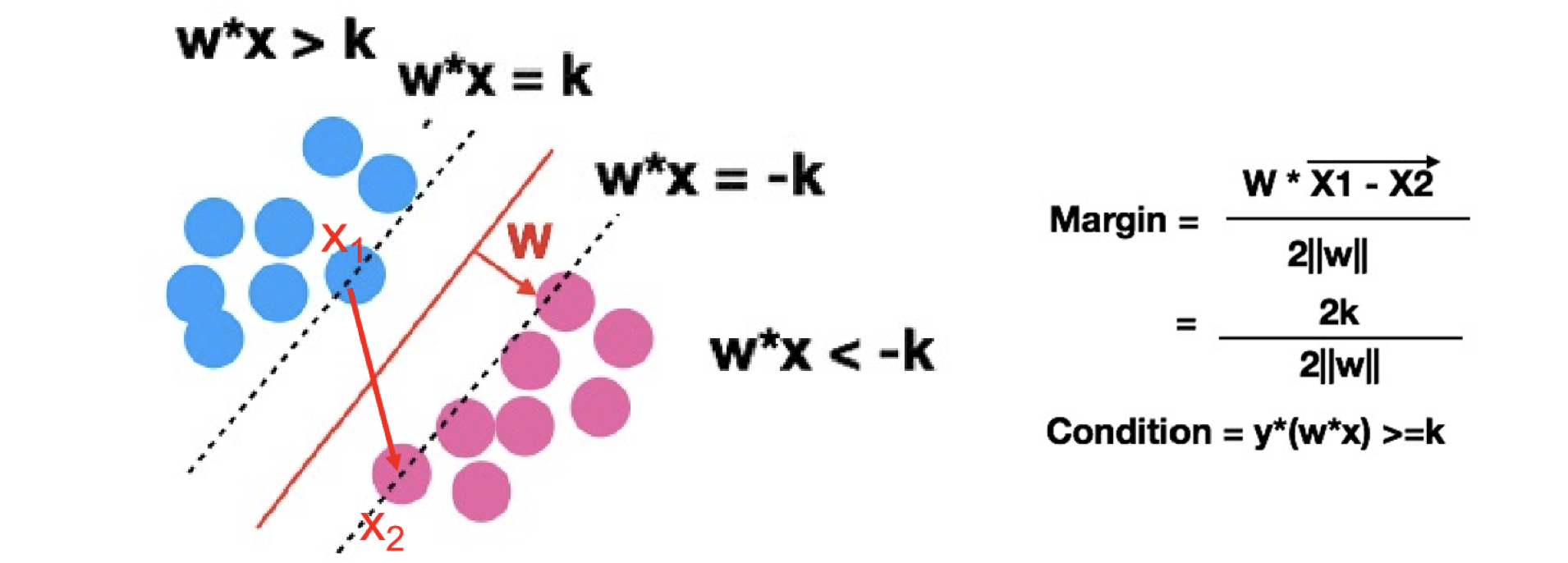
虛線上的點X1,X2 其實就是所謂的支援向量(Support vector),我們主要是利用支援向量來算出Margin,並最大化Margin。那要怎麼計算margin呢? 利用高中數學的知識將X1向量-X2向量得到的向量投影到W就可以了!接下來就是在Y*(W*X) ≥k 的條件下(虛線中間沒有點),來最大化margin reference
SVM的優點是他可以處理多維度的資料,且學習速度快,分類效果也很好,在手寫文字辨別上是目前最好的分類器,不過SVM只能做二元分類
更多閱讀,分類模型的評估
confusion matrix